Logaritmo
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.En matemáticas, el logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante — por identidades logarítmicas — que el logaritmo de un producto es la suma de los logaritmos de los factores:
La noción actual de los logaritmos viene de Leonhard Euler, quien conectó estos con la función exponencial en el siglo XVIII.
Definiciones
- Logaritmo puede ser definido de diversas maneras: como exponente, cuando se conocen la base de una potencia y el valor de esta; tal el caso si
 , como
, como  resuelve la ecuación, se dice que -4 es el logaritmo de 1/16 en base 2. O bien
resuelve la ecuación, se dice que -4 es el logaritmo de 1/16 en base 2. O bien .
.
Se exige que la base de logaritmos sea un número positivo distinto de 1. Usualmente se ha considerado como base, 10: originando los logaritmos decimales o vulgares. O bien la base, el número e: generando los logaritmos naturales o neperianos.
- Como una función real de variable real. Concretamente, considerando que la función exponencial es una función creciente y continua de dominio ℝ y codominio ℝ+, pues tiene función inversa de dominio ℝ+, y codominio ℝ, que también es creciente y continua para base mayor que 1.
- Por integral definida
que se lee logaritmo natural de a, en este caso la base de los logaritmos es el número irracional trascendente e que es el límite de
cuando n tiende a infinito.
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo b(base) se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = logb x, lo que permite obtener n.
(esto se lee como: logaritmo en base b de x es igual a n; si y sólo si b elevado a la n da por resultado a x)
Para que la definición sea válida, no todas las bases y números son posibles. La base b tiene que ser positiva y distinta de 1, luego b> 0 y b ≠ 1, x tiene que ser un número positivo x > 0 y n puede ser cualquier número real (n ∈ R).
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.
Propiedades generales
Los logaritmos, independientemente de la base elegida, cumplen una serie de propiedades comunes que los caracterizan. Así, logaritmo de su base es siempre 1; logb b = 1 ya que b1 = b. El logaritmo de 1 es cero (independientemente de la base); logb 1=0 ya que b0 = 1.
Si el número real a se encuentra dentro del intervalo 0 < a < 1 entonces logb a da un valor negativo o se dice que es un logaritmo negativo. Es evidente, ya que si logaritmo de 1 es cero, entonces valores reales menores que uno serán negativos por ser la función logarítmica estrictamente creciente y cuyo recorrido es (-∞, +∞). También se puede demostrar usando la identidad logarítmica logb(x/y)=logb x - logb y; puesto que a pertenece al intervalo 0 < a < 1, su inverso a-1 será mayor que uno, con lo que logb(a)=logb(1/a-1) = logb 1 - logb(a-1)= -logb(a-1).
Los números negativos no tienen logaritmo en el cuerpo de los reales R, ya que cualquiera que sea el exponente n, se tendrá siempre que bn será mayor que cero, bn > 0; en consecuencia, no hay ningún valor real de n que pueda satisfacer bn = x cuando x sea menor que 0. Sin embargo, este obstáculo se puede salvar, ampliando el dominio de definición al cuerpo de los números complejos C, pudiendo calcular logaritmos de números negativos usando el logaritmo complejo o recurriendo a la formula de Euler.
Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Por ejemplo, las potencias de 2 son 1,2,4,8,16,32,64,..., etc. y sus exponentes serán 0, 1, 2, 3, 4,..., etc. ya que 20 = 1, 21 = 2, 22 = 4, 23 = 8, y 24 = 16, etc. luego log2 1 = 0, log2 2 = 1, log2 4 = 2, log2 8 = 3 y log2 16 = 4, etc.
Identidades logarítmicas
Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un inverso multiplicativo es el inverso aditivo del logaritmo:
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
En realidad la cuarta y quinta identidad son equivalentes, sin más que hacer:
Elección y cambio de base
Entre los logaritmos más utilizados se encuentra el logaritmo natural, cuya base es e, base 10 (logaritmo común), base 2 (logaritmo binario), o en base indefinida (logaritmo indefinido). La elección de un determinado número como base de los logaritmos no es crucial, ya que todos son proporcionales entre sí. Es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto b como k son diferentes de 1):
en la que k es cualquier base válida. Si hacemos k=x, obtendremos:
Base potencia
 si
si 

Empleos
El logaritmo más ampliamente utilizado es el natural, ya que tiene multitud de aplicaciones en física, matemáticas, ingeniería y en ciencias en general. También es bastante utilizado el logaritmo decomal, que se indica como 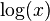 , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), de intensidad de sonido (bH), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.
, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), de intensidad de sonido (bH), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.
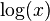 , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), de intensidad de sonido (bH), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.
, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), de intensidad de sonido (bH), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.Propiedades analíticas
Un estudio más profundo de los logaritmos requiere el concepto de función. Un ejemplo es la función que produce la x-ésima potencia de b para cualquier número real x, donde la base (o raíz) b es un número fijo. Esta función se escribe como
Función logarítmica
Para justificar la definición de logaritmos, es necesario mostrar que la ecuación exponencial
tiene una solución x y que esta solución es única, provista de que y es positivo y que b es positivo y distinto de 1. Una demostración de este hecho requiere del teorema del valor intermedio del cálculo elemental. Este teorema establece que una función continua que produce dos valores m y n también produce cualquier valor que se encuentre entre m y n. Una función es continua si esta no «salta», esto es, si su gráfico puede ser escrito sin levantar el lápiz del papel.
Esta propiedad se puede demostrar que se cumple para la función f(x) = bx. Puesto que f toma arbitrariamente valores grandes positivos y valores pequeños positivos, cualquier número y > 0 que se encuentra entre f(x0) y f(x1) para un adecuado x0 y x1. Por lo tanto, el teorema del valor intermedio asegura que la ecuación f(x) = y tiene una solución. Más aún, hay únicamente una solución para esta ecuación, puesto que la función f es estrictamente creciente (para b > 1), o estrictamente decreciente (para 0 < b < 1).
La única solución x es el logaritmo de y en la base b, logb(y). La función que asigna a cada y su logaritmo se llama función logaritmo o función logarítmica (o logaritmo a secas).
Función inversa
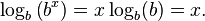 La fórmula para el logaritmo de una potencia dice en particular que para cualquier número x,
La fórmula para el logaritmo de una potencia dice en particular que para cualquier número x,
En lenguaje llano, tomando la x-ésima potencia de b y luego el base-b logaritmo se vuelve a obtener x. De modo contrario, dado un número positivo y, la fórmula
dice que tomando primero el logaritmo y después exponenciando se vuelve a obtener y. Así, las dos maneras posibles de combinar (o componer) logaritmos y exponenciales vuelve a dar el número original. Por lo tanto, el logaritmo en base bes la función inversa de f(x) = bx.
Las funciones inversas están íntimamente relacionadas con las funciones originales. Sus gráficos se corresponden el uno con el otro mediante el intercambio de las coordenadas x e y (o por reflexión sobre la línea diagonal x = y), como se muestra en la figura de la derecha: un punto (t, u = bt) sobre el gráfico de fproporciona un punto (u, t = logbu) sobre el gráfico del logaritmo y viceversa. Como consecuencia, logb(x) diverge a infinito (se hace más grande que cualquier número dado) si x tiende a infinito, siempre queb sea mayor que 1. En ese caso, logb(x) es un función creciente. Para b < 1, logb(x) tiende a menos infinito en lugar de a infinito. Cuando x se aproxima a cero, logb(x) tiende a menos infinito para b > 1 (a más infinito cuando b < 1, respectivamente).
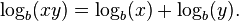
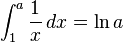


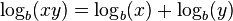

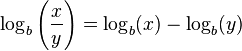
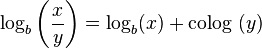
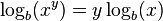
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](https://upload.wikimedia.org/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](https://upload.wikimedia.org/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)
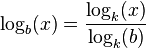
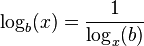
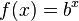

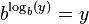
No hay comentarios.:
Publicar un comentario